Introduction to meta-analysis
Meta-analysis is a powerful statistical method used to synthesize and analyze results from multiple research studies, providing a comprehensive and quantitative overview of a specific research question. As a cornerstone of evidence-based practice, meta-analysis plays a crucial role in medical research and other scientific fields. This statistical technique combines data from different studies to increase statistical power and precision in estimating effect sizes.
The importance of meta-analysis in medical research cannot be overstated. It allows researchers to draw more robust conclusions by pooling results from individual studies, which may have limited sample sizes or conflicting outcomes. Meta-analysis is particularly valuable in systematic reviews, where it helps to quantitatively summarize findings across diverse research studies. By applying statistical methods to analyze heterogeneity among studies, meta-analysis can identify patterns and trends that might not be apparent in single studies.
Dissertation Writing Help
Elevate your doctoral journey! Sign up now with Best Dissertation Writers for affordable, top-quality dissertation support. Our expert team will guide you through every step, ensuring your research shines. Don’t wait—start your path to success today!
Meta-analysis is a quantitative synthesis of research findings that goes beyond traditional literature reviews. It employs rigorous statistical analysis to assess the statistical significance of combined results, providing a more objective evaluation of the available evidence. This approach is especially useful in fields where randomized controlled trials are common, as meta analysis of randomized studies can offer the highest level of evidence for clinical decision-making.
In conducting a meta-analysis, researchers must carefully consider study design, literature search strategies, and potential sources of bias. The development of the study protocol, including clear inclusion criteria and sensitivity analyses, is crucial for ensuring the validity and reliability of the meta-analysis results. By systematically addressing these factors, meta-analysis has become an indispensable tool for advancing scientific knowledge and informing evidence-based practice across various disciplines.
What’s the difference between a meta-analysis, systematic review, and literature review?
Meta-analysis, systematic review, and literature review are distinct research synthesis methods, each with unique characteristics and importance in medical research and other fields.
A meta-analysis is a quantitative statistical analysis that combines results from multiple studies to produce a single estimate of effect. Meta-analysis in medical research often focuses on clinical trials and observational studies. It uses statistical methods to calculate summary statistics, assess heterogeneity among studies, and produce forest plots and funnel plots to visualize results. Meta analysis methods include random-effects models and fixed-effects models, which account for variability in study characteristics and populations.
A systematic review follows a rigorous, pre-defined protocol to identify, appraise, and synthesize all relevant studies on a specific research question. It may include a meta analysis if appropriate. Systematic reviews are often conducted using guidelines like the Cochrane Handbook for Systematic Reviews of Interventions or the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA). They involve comprehensive literature searches and may assess the risk of bias in included studies.
A literature review is a broader, often qualitative summary of existing research on a topic. Unlike systematic reviews and meta-analyses, literature reviews may not follow a strict protocol or include statistical analyses.
The choice between these methods depends on the research question and available evidence. Meta-analyses, similar to scoping reviews, provide the highest level of evidence when properly conducted, as they can identify statistically significant effects that may not be apparent in individual studies. Systematic reviews offer a comprehensive overview of evidence, while literature reviews provide a broader context for understanding a research area.
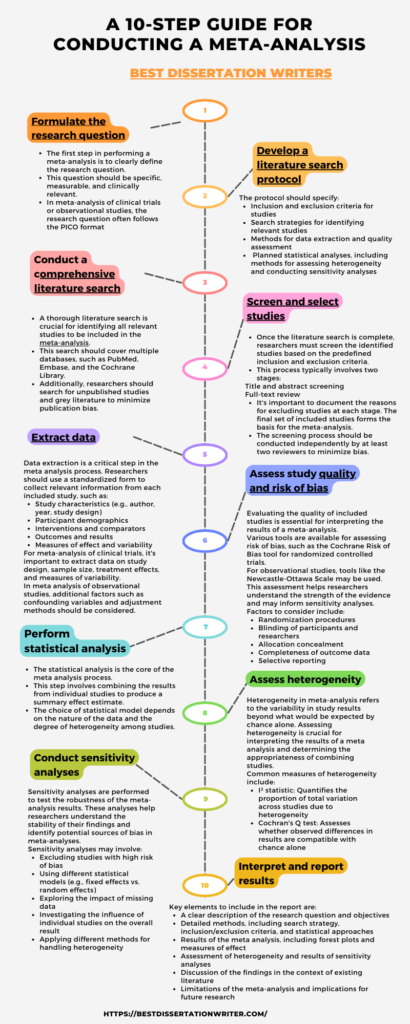
A 10-step guide for conducting a meta analysis
Meta-analysis is a powerful quantitative research synthesis method used extensively in medical research and other scientific fields. As a statistical technique, meta analysis combines results from multiple studies to provide a comprehensive and statistically significant overview of a specific research question. This guide outlines a detailed 10-step process for conducting a meta analysis, emphasizing its importance in health research and clinical decision-making.
Step 1: Formulate the research question
The first step in performing a meta-analysis is to clearly define the research question. This question should be specific, measurable, and clinically relevant. In meta-analysis of clinical trials or observational studies, the research question often follows the PICO format: Population, Intervention, Comparison, and Outcome. A well-formulated question guides the entire meta-analysis process and helps determine the types of studies to be included in the analysis.
Meta-analysis may be used to address various research questions, from evaluating the effectiveness of interventions to estimating the prevalence of health conditions. The research question will inform the study design and the types of studies that will be included in the meta-analysis. This stage also helps in defining the primary purpose of the study, and significance of the review.
Step 2: Develop a literature search protocol
Before conducting the meta analysis, researchers should develop a detailed protocol outlining the study design, methods, and analysis plan. This protocol should be registered with a recognized database, such as the Cochrane Database of Systematic Reviews or PROSPERO. The protocol helps ensure transparency and reduces the risk of bias in meta-analyses.
The protocol should specify:
– Inclusion and exclusion criteria for studies
– Search strategies for identifying relevant studies
– Methods for data extraction and quality assessment
– Planned statistical analyses, including methods for assessing heterogeneity and conducting sensitivity analyses
The development of the study protocol is crucial for ensuring the rigor and reproducibility of the meta-analysis. It also helps to prevent post hoc changes in methodology that could introduce bias.
Step 3: Conduct a comprehensive literature search
A thorough literature search is crucial for identifying all relevant studies to be included in the meta-analysis. This search should cover multiple databases, such as PubMed, Embase, and the Cochrane Library. Additionally, researchers should search for unpublished studies and grey literature to minimize publication bias.
The literature search strategy should be documented in detail to ensure reproducibility. In meta analysis of randomized controlled trials, it’s particularly important to identify all eligible studies to provide the most accurate estimate of treatment effects. For meta-analysis of observational studies, the search may need to be broader to capture diverse study designs.
Step 4: Screen and select studies
Once the literature search is complete, researchers must screen the identified studies based on the predefined inclusion and exclusion criteria. This process typically involves two stages:
1. Title and abstract screening
2. Full-text review
It’s important to document the reasons for excluding studies at each stage. The final set of included studies forms the basis for the meta-analysis. The screening process should be conducted independently by at least two reviewers to minimize bias.
Step 5: Extract data
Data extraction is a critical step in the meta analysis process. Researchers should use a standardized form to collect relevant information from each included study, such as:
– Study characteristics (e.g., author, year, study design)
– Participant demographics
– Interventions and comparators
– Outcomes and results
– Measures of effect and variability
For meta-analysis of clinical trials, it’s important to extract data on study design, sample size, treatment effects, and measures of variability. In meta analysis of observational studies, additional factors such as confounding variables and adjustment methods should be considered.
Step 6: Assess study quality and risk of bias
Evaluating the quality of included studies is essential for interpreting the results of a meta-analysis. Various tools are available for assessing risk of bias, such as the Cochrane Risk of Bias tool for randomized controlled trials. For observational studies, tools like the Newcastle-Ottawa Scale may be used.
Dissertation/Thesis Writing Help
Struggling with your Doctoral or PhD dissertation? Sign up with Best Dissertation Writers and access premium, budget-friendly assistance. Our seasoned professionals will help you craft a compelling thesis that stands out. Take the first step towards your doctorate now!
This assessment helps researchers understand the strength of the evidence and may inform sensitivity analyses. Factors to consider include:
– Randomization procedures
– Blinding of participants and researchers
– Allocation concealment
– Completeness of outcome data
– Selective reporting
The quality assessment should be conducted independently by multiple reviewers to ensure reliability.
Step 7: Perform statistical analysis
The statistical analysis is the core of the meta analysis process. This step involves combining the results from individual studies to produce a summary effect estimate. The choice of statistical model depends on the nature of the data and the degree of heterogeneity among studies.
Common approaches include:
1. Fixed effects model: Assumes all studies are estimating the same true effect size, and any differences are due to sampling error. This model is appropriate when studies are homogeneous.
2. Random effects model: Assumes the true effect size may vary from study to study. This model is often more appropriate when there is significant heterogeneity among studies. Random-effects meta analysis accounts for both within-study and between-study variability.
The meta-analysis estimate is typically presented as a weighted average of the individual study effects, with more precise studies given greater weight. Statistical methods in medical research often involve calculating effect sizes, such as odds ratios, risk ratios, or mean differences, depending on the outcome measure.
Results are often visualized using a forest plot, which displays the effect sizes and confidence intervals for each study, as well as the overall meta-analysis estimate. Funnel plots may be used to assess publication bias.
Statistical significance is typically assessed using p-values and confidence intervals. However, it’s important to consider both statistical and clinical significance when interpreting results.
Step 8: Assess heterogeneity
Heterogeneity in meta-analysis refers to the variability in study results beyond what would be expected by chance alone. Assessing heterogeneity is crucial for interpreting the results of a meta analysis and determining the appropriateness of combining studies.
Common measures of heterogeneity include:
– I² statistic: Quantifies the proportion of total variation across studies due to heterogeneity
– Cochran’s Q test: Assesses whether observed differences in results are compatible with chance alone
If significant heterogeneity is present, researchers may explore its sources through subgroup analyses or meta-regression. Clinical heterogeneity may arise from differences in study populations, interventions, or outcome measures. Statistical heterogeneity may reflect methodological differences or true variability in effect sizes across studies.
Step 9: Conduct sensitivity analyses
Sensitivity analyses are performed to test the robustness of the meta-analysis results. These analyses help researchers understand the stability of their findings and identify potential sources of bias in meta-analyses.
Sensitivity analyses may involve:
– Excluding studies with high risk of bias
– Using different statistical models (e.g., fixed effects vs. random effects)
– Exploring the impact of missing data
– Investigating the influence of individual studies on the overall result
– Applying different methods for handling heterogeneity
In some cases, meta-regression may be used to explore the relationship between study characteristics and effect sizes. This can help identify factors that contribute to heterogeneity in meta analysis.
Step 10: Interpret and report results
The final step in conducting a meta analysis is to interpret the results and prepare a comprehensive report. This report should follow established guidelines, such as the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) statement.
Key elements to include in the report are:
– A clear description of the research question and objectives
– Detailed methods, including search strategy, inclusion/exclusion criteria, and statistical approaches
– Results of the meta analysis, including forest plots and measures of effect
– Assessment of heterogeneity and results of sensitivity analyses
– Discussion of the findings in the context of existing literature
– Limitations of the meta-analysis and implications for future research
When interpreting the results, it’s important to consider both statistical significance and clinical significance. A statistically significant result may not always be clinically meaningful, and vice versa. Researchers should also be cautious about overinterpreting results, especially when the included studies are few or of low quality.
The report should clearly state what the meta analysis can and cannot conclude based on the available evidence. It’s important to acknowledge that meta-analysis cannot overcome fundamental limitations in the primary studies. The quality of a meta-analysis is ultimately dependent on the quality of the included studies.
Advanced meta-analytic techniques
As research synthesis methods continue to evolve, new approaches are expanding the capabilities of meta-analytic techniques. The primary role of the advanced techniques of meta-analysis is to identify consistency and heterogenicity in the existing literature. Some advanced methods include:
1. Network meta-analysis: Allows for simultaneous comparison of multiple interventions, even when direct comparisons are not available in primary studies.
2. Individual participant data meta analysis: Uses raw data from original studies, allowing for more detailed and flexible analyses.
3. Meta-analysis of rare events: Employs specialized methods to synthesize data on low-frequency outcomes.
4. Bayesian meta-analysis: Incorporates prior information and allows for more flexible modeling of heterogeneity. This approach is key for assessing variability in study design.
These advanced techniques can provide deeper insights into treatment effects across different populations and settings, and may be particularly useful in complex research scenarios.
Importance of meta-analysis in medical research
Meta-analysis plays a crucial role in evidence-based medicine and health research. Its importance can be summarized in several key points:
1. Increased statistical power: By combining multiple studies, meta analysis can detect effects that may not be apparent in individual studies, particularly for rare outcomes or small effect sizes.
2. Improved precision: Meta-analysis provides more precise estimates of effect sizes than individual studies alone.
3. Resolving conflicts: When individual studies have conflicting results, meta analysis can help determine the overall direction and magnitude of an effect.
4. Generalizability: By including studies from diverse populations and settings, meta analysis can assess the consistency of effects across different contexts.
5. Identifying research gaps: Systematic reviews and meta-analyses can highlight areas where evidence is lacking, guiding future research efforts.
6. Informing clinical practice: The results of meta-analyses often inform clinical guidelines and decision-making.
7. Efficient use of resources: Meta-analysis allows researchers to synthesize existing data, potentially reducing the need for new, large-scale studies.
Limitations and considerations in meta-analysis
While meta analysis is a powerful tool, it’s important to recognize its limitations:
1. Quality of primary studies: Meta-analysis cannot overcome fundamental flaws in the included studies.
2. Publication bias: Despite efforts to include unpublished data, meta-analyses may be affected by the tendency for positive results to be published more often than negative ones.
3. Heterogeneity: When studies are too diverse in their methods or populations, it may not be appropriate to combine them in a meta-analysis.
4. Ecological fallacy: Conclusions drawn from group-level data may not apply to individuals. Results from the review are diverse and can be used for understanding the relationship between independent and dependent variables’ effect in meta-analysis of published evidence.
5. Outdated results: As new studies are published, the results of a meta analysis may become outdated.
Meta-analysis is a sophisticated statistical method that plays a vital role in synthesizing evidence across multiple studies. By following this 10-step guide and considering the advanced techniques and limitations discussed, researchers can conduct rigorous meta-analyses that contribute valuable insights to medical research and clinical practice.
As the volume of published research continues to grow, the importance of meta-analysis in summarizing and interpreting evidence is likely to increase. This has called for the need for meta analysis based assessed of evidence quality. However, it’s crucial that meta-analyses are conducted with careful attention to methodological rigor and transparency to ensure their results are reliable and meaningful.
Meta-Analysis Help
Unlock your full potential! Register with Best Dissertation Writers for unparalleled dissertation support. Our affordable, high-quality services cater to all doctoral needs. Don’t let your PhD dreams stall—sign up and excel in your research today!
When performed correctly, meta-analysis provides a powerful tool for advancing scientific knowledge, informing clinical practice, and ultimately improving patient care. As such, it remains a cornerstone of evidence-based medicine and a critical component of the modern research landscape.
Data analysis techniques in meta-analysis
Meta-analysis is a quantitative research synthesis method that combines results from multiple studies to provide a comprehensive statistical analysis of a specific research question. In meta analysis in medical research and other fields, various data analysis techniques are employed to synthesize evidence and draw robust conclusions. This article explores the key data analysis techniques used in meta-analysis, highlighting their importance in systematic reviews and medical research methodology.

Meta-analysis is the statistical combination of results from multiple studies, allowing researchers to identify patterns and effects that may not be apparent in individual studies. The development of meta analysis techniques has revolutionized how we approach systematic literature reviews, providing a rigorous framework for quantitatively summarizing research findings.
Effect size calculation
The first step in meta-analysis is calculating effect sizes for each study included in the meta analysis. Effect sizes represent the magnitude and direction of the relationship between variables or the difference between groups. Common effect size measures include standardized mean differences, odds ratios, and risk ratios. The choice of effect size measure depends on the study design and the nature of the outcome data.
Fixed-effect vs. Random-effects models
Meta-analysis models can be broadly categorized into fixed-effect and random-effects models. The choice between these models depends on the assumed heterogeneity among studies.
1. Fixed-effect model: This model assumes that all studies in the meta-analysis are estimating the same true effect size, and any differences are due to sampling error alone.
2. Random-effects model: This model assumes that the true effect size may vary from study to study due to differences in populations, interventions, or other factors. Random-effects meta analysis accounts for both within-study and between-study variability.
The decision between fixed-effect and random-effects models is crucial, as it affects the weighting of individual studies and the interpretation of results in meta analysis.
Assessing heterogeneity
Heterogeneity in meta-analysis refers to the variability in study results beyond what would be expected by chance alone. Assessing heterogeneity is critical for determining the appropriateness of combining studies and interpreting results. Common methods for assessing heterogeneity include:
1. Cochran’s Q test
2. I² statistic
3. Tau² statistic
When significant heterogeneity is detected, researchers may explore its sources through subgroup analyses or meta-regression.
Meta-regression
Meta-regression is an extension of meta-analysis that allows researchers to examine the relationship between study-level characteristics and effect sizes. This technique in a meta analysis study may can help identify sources of heterogeneity and explore how study characteristics influence outcomes. Meta-analysis and meta-regression can be performed using fixed-effect or random-effects models, depending on the underlying assumptions about heterogeneity.
Sensitivity analyses
Sensitivity analyses are crucial for assessing the robustness of meta-analysis results in each of the included empirical study. These analyses involve systematically altering aspects of the meta analysis to determine whether the results remain consistent. Sensitivity analyses help researchers understand the stability of their findings and identify potential sources of bias in studies included in a meta-analysis. systematic review or meta-analysis play a central role of assessing and reporting quality of evidence in the existing literature.
Publication bias assessment
Publication bias can distort meta-analysis findings based on the adopted methods of meta-analysis. Techniques for assessing publication bias include funnel plots, Egger’s test, and the trim and fill method. All these are important in assessing the quality of evidence reported in all of the studies in a meta analysis. Addressing publication bias is essential for ensuring the validity of meta analysis results.
Network meta-analysis
Network meta-analysis is an advanced technique that allows for the simultaneous comparison of multiple interventions, even when direct comparisons are not available in primary studies. This method combines direct and indirect evidence to rank interventions and estimate comparative effectiveness. This method is widely used in the BMC medical research methodology to assess quality of evidence in the studies included in a review.
Classical meta-analysis vs. Advanced techniques
While classical meta-analysis remains a cornerstone of research synthesis, advanced techniques like network meta-analysis and Bayesian methods are increasingly used to address complex research questions. These methods allow for more flexible modeling and can provide additional insights beyond what classical meta analysis can offer and help in ensuring that every included study is represented in the final analysis or as a study group. Evidence in the studies in meta-analysis can also assessed using qualitataive systematic review.
Importance of data analysis techniques in meta-analysis
The proper application of data analysis techniques in meta-analysis is crucial for several reasons:
1. Rigorous synthesis: Meta-analysis provides a systematic and quantitative approach to synthesizing research findings, allowing for more objective conclusions than narrative reviews.
2. Increased statistical power: By combining multiple studies, meta analysis can detect effects that may not be apparent in individual studies, particularly for rare outcomes or small effect sizes.
3. Exploration of heterogeneity: Advanced techniques like meta-regression allow researchers to investigate sources of variability across studies, providing insights into factors that influence treatment effects.
4. Assessment of bias: Methods for detecting and adjusting for publication bias help ensure the validity of meta analysis results.
5. Informing clinical practice: The results of meta-analyses often inform clinical guidelines and decision-making, making the accurate application of statistical methods crucial for patient care.
6. Guiding future research: By identifying gaps and inconsistencies in existing evidence, meta-analyses can guide the development of future studies and research agendas.
Meta-analysis methods are continually evolving, with new approaches being developed to address the challenges of synthesizing diverse and complex research studies. For example, methods for meta analysis of rare events and individual participant data meta-analysis are expanding the capabilities of research synthesis.
The choice of meta-analysis model involves careful consideration of the study characteristics, heterogeneity, and research question. Researchers must be aware of the strengths and limitations of each approach to ensure appropriate application and interpretation of results.
Meta-analysis is performed using specialized software, such as Review Manager (RevMan) or comprehensive statistical packages. These tools facilitate the implementation of various meta-analysis techniques and the production of forest plots, funnel plots, and other visualizations essential for presenting meta-analysis results.
In conclusion, data analysis techniques in meta-analysis play a vital role in the systematic review process and are essential for generating reliable and meaningful results. As the field of meta analysis continues to evolve, researchers must stay informed about the latest methodological developments to ensure the highest standards of evidence synthesis in medical research and beyond. By leveraging these powerful analytical tools, meta-analysis can provide crucial insights to guide clinical practice, inform health policy, and advance scientific knowledge.
A generic inverse-variance approach to meta-analysis
Meta-analysis is a powerful statistical method used to combine results from multiple studies, providing a comprehensive synthesis of available evidence. One of the most widely used techniques in meta-analysis is the generic inverse-variance approach. This method is particularly valuable in meta-analysis of medical research and other fields where studies may have different designs or report different effect measures.
The generic inverse-variance approach to meta analysis is a statistical method that allows researchers to combine study results by weighting each study according to its precision. This technique is especially useful when studies included in a meta-analysis report different effect measures or when individual participant data are not available. The approach can be applied to both fixed-effect and random-effects meta-analysis models, making it a versatile tool in research synthesis.
In this method, each study included in the meta-analysis is represented by an effect estimate and its standard error. The effect estimate could be a mean difference, standardized mean difference, log odds ratio, log risk ratio, or any other appropriate measure, depending on the study design and outcome type. The inverse of the squared standard error is used as the study weight, giving more precise studies (those with smaller standard errors) greater influence on the overall meta-analysis estimate.
The generic inverse-variance approach is particularly important in meta-analysis for several reasons:
1. Flexibility: It can be used with various types of effect measures, allowing for the inclusion of diverse study designs in a single meta-analysis.
2. Handling of different study designs: This method enables the combination of results from randomized controlled trials, observational studies, and other study types within the same meta analysis.
3. Incorporation of adjusted estimates: When studies report adjusted effect estimates (e.g., from multivariable analyses), these can be easily incorporated into the meta-analysis using this approach.
4. Applicability to both fixed-effect and random-effects models: The generic inverse-variance method can be used with both types of meta-analysis models, allowing researchers to account for potential heterogeneity among studies.
To perform a meta analysis using the generic inverse-variance approach, researchers follow these steps:
1. Extract effect estimates and their standard errors from each study included in the meta-analysis.
2. Calculate the weight for each study as the inverse of the squared standard error.
3. Compute the weighted average of the effect estimates across all studies.
4. Calculate the standard error of the pooled estimate.
5. Derive confidence intervals and assess statistical significance of the overall effect.
Dissertation Writing Help
Transform your dissertation from daunting to done! Sign up with Best Dissertation Writers for top-tier, cost-effective guidance. Our expert team will help you navigate complex research challenges. Start your journey to doctoral success now!
When heterogeneity is present among the studies in a meta-analysis, a random-effects model using the generic inverse-variance approach may be more appropriate. This model assumes that the true effect sizes vary across studies and incorporates this additional variability into the analysis.
The generic inverse-variance approach can also be extended to meta-regression, allowing researchers to explore potential sources of heterogeneity by examining the relationship between study-level characteristics and effect sizes.
In conclusion, the generic inverse-variance approach is a fundamental technique in meta-analysis, offering a flexible and robust method for combining results across studies. Its ability to handle diverse effect measures and study designs makes it an essential tool in systematic reviews and meta-analyses, particularly in medical research where evidence often comes from a variety of study types. By employing this method, researchers can conduct comprehensive and statistically sound meta-analyses, contributing to the development of evidence-based practice and informed decision-making in healthcare and other fields.
Frequently asked questions about meta-analysis
What is the difference between a systematic review and a meta-analysis?
A systematic review and a meta-analysis are both methods of research synthesis, but they differ in their approach and output. A systematic review is a comprehensive, structured literature search and critical appraisal of studies addressing a specific research question. It follows a predefined protocol to identify, select, and summarize all relevant research.
On the other hand, a meta-analysis is a statistical technique used within a systematic review to quantitatively combine and analyze results from multiple studies. While a systematic review may or may not include a meta-analysis, a meta-analysis is always part of a systematic review.
The key difference is that a systematic review provides a qualitative summary of evidence, while a meta-analysis offers a quantitative statistical synthesis of data. Meta-analysis can provide more precise estimates of effect sizes and explore sources of heterogeneity among studies.
How to do a meta-analysis example?
To conduct a meta-analysis, follow these steps using an example of analyzing the effectiveness of a new drug for hypertension:
- Formulate a clear research question: “Is the new drug effective in reducing blood pressure compared to placebo?”
- Define inclusion criteria: randomized controlled trials comparing the drug to placebo in adults with hypertension.
- Conduct a comprehensive literature search across multiple databases.
- Screen studies and extract data on sample sizes, mean blood pressure reductions, and standard deviations.
- Calculate effect sizes (e.g., standardized mean differences) for each study.
- Choose a meta-analysis model (fixed-effect or random-effects) based on heterogeneity assessment.
- Perform the meta-analysis using statistical software, weighting studies by their inverse variance.
- Generate a forest plot to visualize results and calculate an overall effect size with confidence intervals.
- Assess publication bias using funnel plots and statistical tests.
- Interpret results and discuss implications for clinical practice.
What is a meta-analysis for dummies?
A meta-analysis for dummies can be explained as a statistical method to combine results from multiple scientific studies to get a bigger picture. Imagine you’re trying to find out if a new diet works. Instead of just looking at one study, you gather all the studies about this diet. Each study is like a piece of a puzzle.
Meta-analysis is the process of putting these pieces together to see the whole picture. It’s like calculating an average, but it’s more sophisticated because it takes into account how reliable each study is.
Studies with more participants or better methods are given more weight. The result is a more powerful and precise estimate of whether the diet really works. Meta-analysis helps to resolve conflicts between studies and can find effects that individual studies might miss.
What is the data of meta-analysis?
The data used in meta-analysis typically comes from primary research studies addressing a common research question. This data includes:
- Effect sizes: Measures of the strength and direction of relationships or interventions (e.g., mean differences, odds ratios, correlation coefficients).
- Sample sizes: The number of participants in each study.
- Measures of variability: Standard deviations, standard errors, or confidence intervals.
- Study characteristics: Information about study design, population, interventions, and outcomes.
- Quality assessments: Evaluations of study rigor and potential biases.
- Moderator variables: Factors that might influence the effect sizes across studies.
Meta-analysts extract this data from published studies, unpublished reports, or by contacting study authors. The data is then standardized and combined using statistical methods to produce an overall effect estimate and explore heterogeneity among studies. This aggregated data allows for more powerful and generalizable conclusions than individual studies alone can provide.
